Question Bank

(a) Differentiate $f(x)=\sqrt{(4-9x^4)}$.

*You do not need to simplify your answer.*

(b) A curve is defined by the equation $y=(x^2+3x+2)\sin x$.

Find the gradient of the tangent to this curve when $x=0$.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(c) For the function below, find the range of values of $x$ for which the function is decreasing.

$y = 3(2x-7)^2 + 60\ln x + 12,\ x>0$

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(d) Find the $x$-value(s) of any stationary points on the graph of the function below, and determine their nature.

y = (2x - 1)e^{-2x}

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(e) A curve is defined by the equation $y=\dfrac{2x^2-1-2x\ln x}{x}$, where $x>0$.

The curve has a point of inflection at the point P.

Find the equation of the tangent to the curve at the point P.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(a) Differentiate $y=\sqrt{x}\cdot \sec(6x)$.

*You do not need to simplify your answer.*

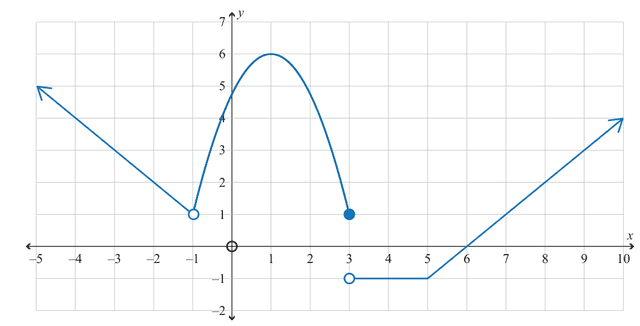
(b) The graph below shows the function $y=f(x)$.



(i) For the function above, find the value(s) of $x$ where $f(x)$ is continuous but not differentiable.

(ii) For the function above, find the value(s) of $x$ where $f'(x)=0$.

(iii) What is the value of $\lim_{x\to -1} f(x)$?

State clearly if the value does not exist.

(c) Find the $x$-value(s) of any stationary point(s) on the graph of the function $f(x)=\dfrac{x^2-5x+4}{x^2+5x+4}$.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

*You do not need to determine the nature of any stationary point(s) found.*

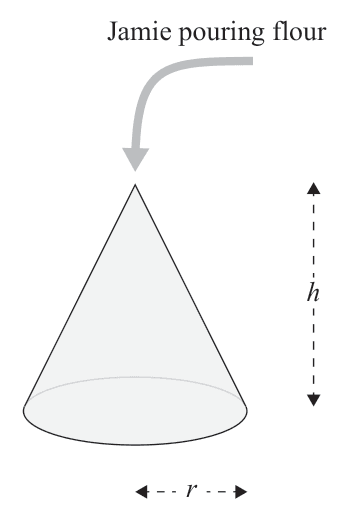
(d) Jamie is doing some baking and pouring the flour to form a conical pile.

The height of the pile is always the same as the diameter of the base of the cone.

If the flour is being added at a constant rate of $3\text{ cm}^3$ per second, at what rate is the height increasing when the pile is $4\text{ cm}$ in height?

*You must use calculus and show any derivatives that you need to find when solving this problem.*

Note that volume of a cone $=\dfrac{1}{3}\pi r^2h$.

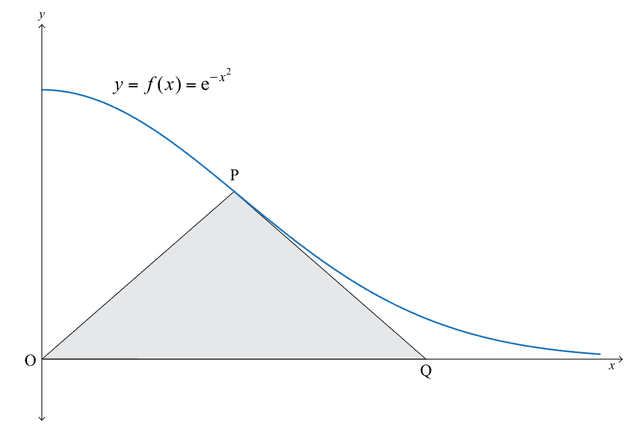
(e) The diagram below shows part of the graph of the function $f(x)=e^{-x^2}$, where $x\ge 0$.



The point P lies on the curve and the point Q lies on the $x$-axis so that OP = PQ, where O is the origin.

Prove that the largest possible area of the triangle OPQ is $\frac{1}{\sqrt{2e}}$.

*You do not need to show that the area you have found is a maximum.*

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(a) A function is defined parametrically by the pair of equations:

$x = 3t^2 + 1$ and $y = \cos t$.

Find an expression for $\dfrac{dy}{dx}$.

(b) An object is travelling in a straight line. Its displacement, in metres, is given by the formula

$s(t)=\ln(3t^2+5t+2)$, where $t>0$ and $t$ is time, in seconds.

Find the velocity of this object when $t=1$ second.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(c) Show that $y=\sin(x^2)-\cos(x)$ is a solution to the equation

$\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}+4x^2y=2\cos(x^2)+(1-4x^2)\cos x.$

(d) Consider the function $f(x)=\dfrac{\ln x}{x}$, $x>0$.

Find the coordinates of the point of inflection on the graph of the function.

*You can assume that your point found is actually a point of inflection.*

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(e) The graph of the function $y=\dfrac{xe^{3x}}{2x+k}$, where $k$ is a non-zero constant, has a single turning point at Q.

Find the $x$-coordinate of the point Q.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(a) Differentiate $y=\sqrt{3x-2}$.

*You do not need to simplify your answer.*

(b) Find the rate of change of the function $f(t)=t^2e^{2t}$ when $t=1.5$.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

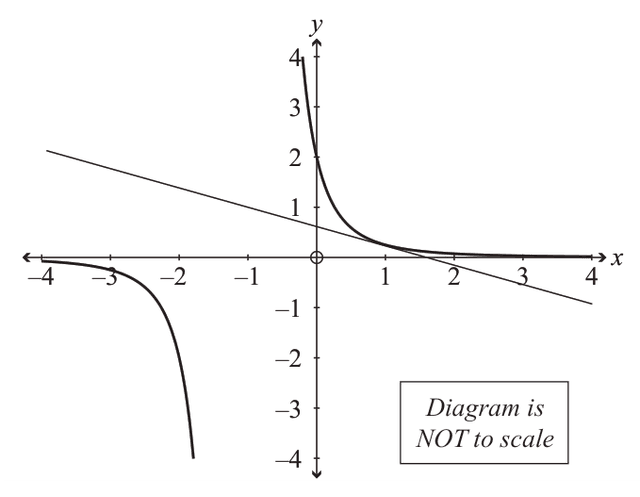
(c) The graph shows the curve $y=\dfrac{2}{(x+1)^3}$, along with the tangent to the curve drawn at $x=1$.



A second tangent to this curve is drawn which is parallel to the first tangent shown in the diagram.

Find the $x$-coordinate of the point where this second tangent touches the curve.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

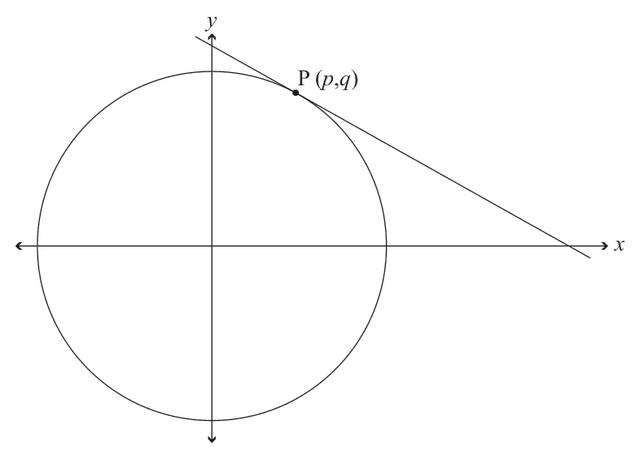
(d) The diagram below shows a tangent passing through the point P $(p,q)$ which lies on the circle with parametric equations $x=4\cos\theta$ and $y=4\sin\theta$.



Show that the equation of the tangent line is $px+qy=p^2+q^2$.

(e) The graph of $y=x(x-2m)^2$, where $m>0$, is shown.
The total shaded area between the curve and the $x$-axis from $x=0$ to $x=2m$ is given by $A=\dfrac{4m^4}{3}$.

A right-angled triangle is now constructed with one vertex at $(0,0)$ and another on the curve $y=x(x-2m)^2$, as shown below.



Show that the maximum area of such a triangle is $\dfrac{3}{8}$ of the total shaded area.

*You must use calculus and show any derivatives that you need to find when solving this problem.*
*You do not have to prove that the area you have found is a maximum.*

(a) Differentiate $y=\ln(x^2-x^4+1)$.

You do not need to simplify your answer.

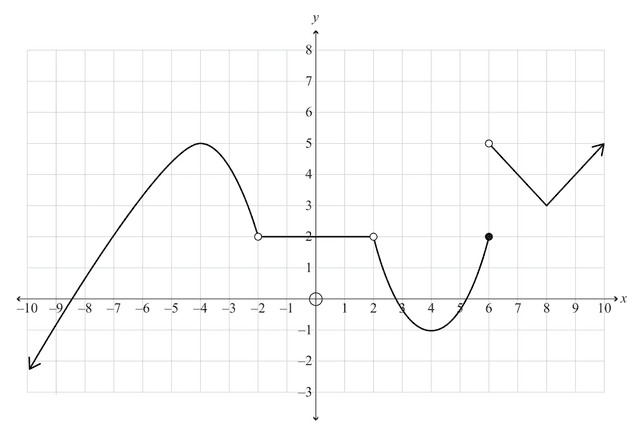
(b) The graph below shows the function $y=f(x)$.



For the function above:

(i) Find the value(s) of $x$ where $f(x)$ is continuous but not differentiable.

(ii) Find the value(s) of $x$ where $f'(x)=0$ and $f''(x)<0$ are both true.

(iii) What is the value of $\lim_{x\to 6} f(x)$?

State clearly if the value does not exist.

(c) Char goes for a ride on a Ferris wheel. As she rotates around, her position can be described by the pair of parametric equations:

$x=5\sqrt{2}\sin\left(\frac{\pi t}{5}\right)$ and $y=10-5\sqrt{2}\cos\left(\frac{\pi t}{5}\right)$

where $t$ is time, in seconds, from the start of the ride.

Find the gradient of the normal to this curve at the point when $t=6.25$ seconds, after the start of the ride.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(d) Find the co-ordinates of any stationary points on the graph of the function $f(x)=\frac{1}{x}-\frac{2}{x^3}$, identifying their nature.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(e) A power line hangs between two poles.

The equation of the curve $y=f(x)$ that models the shape of the power line can be found by solving the differential equation:

$$a\,\frac{d^{2}y}{dx^{2}}=\sqrt{1+\left(\frac{dy}{dx}\right)^{2}}$$

Use differentiation to verify that the function $y=\dfrac{a}{2}\left(e^{\frac{x}{a}}+e^{-\frac{x}{a}}\right)$ satisfies the above differential equation, where $a$ is a positive constant.

(a) Differentiate $f(x)=\dfrac{x^2}{\cos x}$.

*You do not need to simplify your answer.*

(b) Find the gradient of the tangent to the curve $y=\cot(2x)$ at the point where $x=\frac{\pi}{12}$.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(c) A curve is defined by the equation $f(x)=\dfrac{e^x}{x^2+2x}$.

Find the $x$-value(s) of any point(s) on the curve where the tangent to the curve is parallel to the $x$-axis.

*You must use calculus and show any derivatives that you need to find when solving this problem.*

(d) Find the $x$-value(s) of any points of inflection on the graph of the function $f(x)=3x^2\ln(x)$.

You can assume that your point(s) found are actually point(s) of inflection.

You must use calculus and show any derivatives that you need to find when solving this problem.

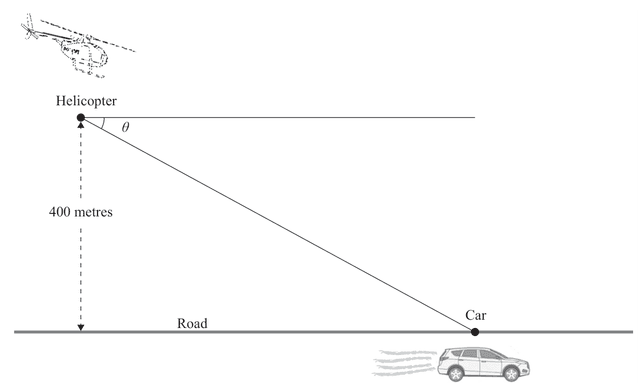
(e) A police helicopter is flying above a straight horizontal section of motorway chasing a speeding car.

The helicopter is flying at a constant speed of $72\text{ m s}^{-1}$ and at a constant height of $400$ metres above the ground. The helicopter is attempting to catch up with the car.

When the direct distance from the helicopter to the car is $2500$ metres, the angle of depression, $\theta$, between the horizontal and the line of sight from the helicopter to the car is increasing at a rate of $0.002\text{ rad s}^{-1}$.



Calculate the speed of the car at this instant.

*You must use calculus and show any derivatives that you need to find when solving this problem.*